Physics Objects Information
With Microsoft Flight Simulator 2024, each of the parts of an aircraft can be defined as specific physics objects permiting much greater control over their properties and their flight model behavior. This page contains various notes related to some of the functionality derived from the flight_model.cfg sections and parameters related specifically to these physics objects within the simulation (for example [OBJ_EA1_FUSELAGE.N] or [OBJ_AIRGEO_VTAIL]).
Note On Surface Cx
When it comes to defining the surfaces of your aircraft using the various [OBJ_EA1_*] and [OBJ_AIRGEO_*] sections of the flight model (for example [OBJ_EA1_FUSELAGE.N]), there are a number of parameters available which are used to create the lift and drag curves for the surfaces of the object being created. Each of these parameters have X (lateral), Y (vertical) and Z (longitudinal) components, since the surface can be positioned in 3D space, and the values used will be one or the other (or interpolated) depending on the position of the surface within the object definition. Note that these positions are all calculated relative to the Datum Reference Point. For example, if we consider a fuselage object:
- The X-axis (lateral, \(C_y\)) component defines how the surface will behave when on the sides of the fuselage.
- The Y-axis (vertical, \(C_n\)) component defines how the surface will behave when on the top and bottom of the fuselage.
- The Z-axis (longitudinal, \(C_a\)) component defines how the surface will behave when on the front and back of the fuselage.
- Any surface that is between these axis will use interpolated values, based on it's position.
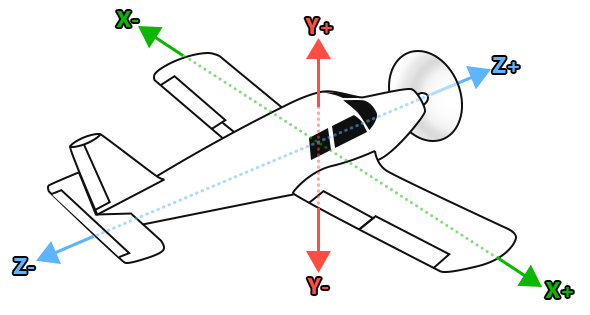
The 4 different surface \(C_x\) values will use the appropriate component (X, Y, or Z) to calculate how the surface should react to the incoming airflow, depending on the position of the surface. These parameters are:
surface_cx- The friction - or drag coefficient - of the surface when the airflow / relative wind direction is close to the tangent to the surface. During normal flight, for the front facing surfaces of the fuselage, this parameter plays no role. For the side and top / bottom facing surfaces however, this will impact the global drag and sideforce of the aircraft when the aircraft slips or pitches up or down. For the top / bottom surfaces of the object, this also plays the role of the lift coefficient. In the case of the top-down surfaces of the fuselage, this describes the lift coefficient of the fuselage surfaces.
surface_cx_tangent- The friction - drag coefficient - when the airflow is at a perfect tangent to the surface. This is used to model imperfections on the surface, like old paint, scratches, etc... This parameter plays no role when the air is coming from a normal / perpendicular direction.
surface_cx_normal- The friction - or drag coefficient - of the surface when the airflow / relative wind direction is perpendicular to the surface. During normal flight, for the forward facing surfaces of the fuselage, this would be the drag coefficient. For the side-facing surfaces, this would be the drag coefficient when the airflow comes from the side, ie: when still on the ground or taxiing in a strong side wind. The same principle applies to wind coming from above or below the aircraft and hitting the top or bottom surfaces.
surface_cx_efficiency- this parameter works with thesurface_cxparameter. When the surface starts to have some incidence with the airflow, thesurface_cxapplies to lift but will also generate some drag. Thesurface_cx_efficiencyparameter allows you to define how much drag will be generated. This is the equivalent of induced drag for wings, but occurs for all surfaces of the aircraft with airflow coming from any direction.

Note On Physics Groups
Most of the available physics objects that can be created as part of the Microsoft Flight Simulator 2024 can be assigned to one or more groups. This is done through the group parameter (as listed in the object parameters for example: [OBJ_EA1_FUSELAGE.N]) of each object. By themselves, the group tags will have no direct impact on the simulation and are instead designed to be used in debugging and user-made tools. The built-in group tags are as follows:
The following debugging tools will use these groups as part of the way they gather debug information:
- The plane engine simulation measures propeller absorbed torque in the Engines debug window by looking at surfaces in the
bladegroup. - The helicopter engine simulation measures rotor absorbed torque in the Engines debug window by looking at surfaces in the
bladegroup. The main rotor and secondary/tail rotor are differentiated using thepNgroup, wherep0is the main rotor andp1is the secondary or tail rotor. - The plane propeller thrust force and moment debugging in the Engines debug window looks for surfaces with the
bladegroup. - For aircraft with surfaces that you want included in the data of the Sim Wind Tunnel debug window should be included in the group tag
extairframe. - To get debug data on helicopter rotor operations using the Engines debug window, you should include the following group tags:
root,typical,tip, andblade. - To include physics object surfaces in the Stall debug window data, use the
wing,tip,left,inner,right, andextairframegroup tags.
Groups And SimVars
The following SimVars will return information based on the groups assigned to the various surface objects:
WINDSHIELD WIND VELOCITY- This SimVar will derive it's value a surface that belongs to thefuselageandtipgroups. If there are no such surfaces available, it will use thecentergroup.
INCIDENCE ALPHA- This SimVar will return the angle of attack of different surfaces based on the supplied group ID value where:- 0 = the
centergroup - 1 = the surface objects that belongs to
wing,left, andtipgroups (ie: the left wing surface), or thecentergroup if there are no surfaces that meet the initial group criteria. - 2 = the surface objects that belongs to
wing,right, andtipgroups (ie: the right wing surface), or thecentergroup if there are no surfaces that meet the initial group criteria.
- 0 = the
Note On The Inertia Tensor
The empty_inertia_tensor parameter represents the full inertia tensor of an empty aircraft. This inertia tensor is a symmetric 3×3 matrix, as shown below:
$$\textrm{Inertia tensor} =
\begin{bmatrix}
J_{xx} & J_{xy} & J_{xz} \\
J_{yx} & J_{yy} & J_{yz} \\
J_{zx} & J_{zy} & J_{zz}
\end{bmatrix}$$
The elements on the main diagonal of this matrix are the following main moments of inertia relative to the aircraft CG:
- \(J_{xx}\) - the pitch moment of inertia around the lateral X aircraft axis in the MSFS 2024/DirectX convention.
- \(J_{yy}\) - the yaw moment of inertia around the vertical Y aircraft axis in the MSFS 2024/DirectX convention.
- \(J_{zz}\) - the roll moment of inertia around the longitudinal Z aircraft axis in the MSFS 2024/DirectX convention.
All of the off-diagonal elements represent the centrifugal moments of inertia, and - since the inertia matrix is always symmetrical - only three of the six off-diagonal elements are actually unique:
- \(J_{xy}\) = \(J_{yx}\) = the centrifugal moment of inertia with respect to the lateral-vertical plane.
- \(J_{xz}\) = \(J_{zx}\) = the centrifugal moment of inertia with respect to the lateral-longitudinal plane.
- \(J_{yz}\) = \(J_{zy}\) = the centrifugal moment of inertia with respect to the longitudinal-vertical plane.
These values should be described using the standard mathematical convention:
$$J_{xy} = J_{yx} = (-m) \times x \times y$$
$$J_{xz} = J_{zx} = (-m) \times x \times z$$
$$J_{yz} = J_{zy} = (-m) \times y \times z$$
Where \(x\), \(y\), and \(z\) are the coordinates of an elementary mass \(m\) relative to the aircraft CG.
IMPORTANT! Using an alternative convention - with positive \(m\) instead of negative - is not supported and may cause validity checks to fail, leading to incorrect aircraft behavior in the simulation.
Tensor Validity Checks
The inertia tensor of an aircraft must satisfy specific mathematical criteria, and if these criteria are violated, the tensor tends to define an aircraft that cannot exist in the "real" world, and thus will have issues in the simulation. Therefore, when loading the aircraft mass properties in Microsoft Flight Simulator 2024, a set of validity checks will be performed on the empty aircraft inertia tensor provided via the empty_inertia_tensor parameter.
- If the tensor passes all checks, the parameter is accepted as "valid" and will be used in multiple areas of the simulation (see the section Tensor Effects, below).
- If the tensor is found to be "invalid" (i.e. it does not represent a physically possible object), the new parameter is ignored, warning messages are logged to the console, and the
empty_weight_pitch_MOI,empty_weight_roll_MOI,empty_weight_yaw_MOI, and the optionalempty_weight_coupled_MOIparameters will be used as a fallback (these will also be used if the tensor parameter is not defined). These parameters will also be subject to the same validity checks, but will not block the build process or prevent the aircraft from flying if they fail the check.
Note that the inertia tensor is validated based on the principal, not main, moments of inertia, which must satisfy the following two conditions:
- All three principal moments of inertia must be positive. Note that the principal moments of inertia are not always the same as the main moments of inertia, since for any physical body there is always a rotation from one coordinate system to another coordinate system, such that in the new coordinate system the tensor of inertia becomes diagonal:
$$\textrm{Inertia tensor} =
\begin{bmatrix}
J_{xx} & 0 & 0 \\
0 & J_{yy} & 0 \\
0 & 0 & J_{zz}
\end{bmatrix}$$Therefor the principal MOI, are - by definition - the main MOI when (in a certain coordinate system) all centrifugal moments of inertia are zero. That is, when the inertia tensor is a diagonal matrix.
- The triangle inequality must hold for the principal moments of inertia. The triangle inequality principle states that for any rigid body, the sum of any two principal moments of inertia must always be greater than the third. So, mathematically, if \(J_x\), \(J_y\), and \(J_z\) are the principal moments of inertia, then:
$$J_x + J_y > J_z$$
$$J_x + J_z > J_y$$
$$J_y + J_z > J_x$$
So, to perform the checks mentioned above, MSFS 2024 now first finds the rotation of the original inertia tensor, in order to determine the principal moments of inertia.
Tensor Effects
If the empty_inertia_tensor parameter is present and valid (see Tensor Validity Checks), then it will activate the following effects in the simulation:
- The addition of payload stations (see
station_load.N) will correctly affect the aircraft moments of inertia by updating the full inertia tensor matrix accordingly (in previous versions of the simulation, all payload stations were merged into a single equivalent mass before being added to the aircraft, which led to incorrect accounting for the effect of spatially separated masses on the moments of inertia). If you are editing a legacy aircraft which had compensated for this by increasing the empty aircraft MOIs, a re-adjustment may be necessary when you use the inertia tensor.
- In previous versions of the simulation, any additional terms to moments of inertia were calculated relative to the CG of the empty aircraft, but using the inertia tensor now means that calculations will be made relative to the actual CG, which shifts as the mass distribution changes due to things like fuel consumption, payload changes, etc...
- The full 3×3 inertia tensor matrix is used for aircraft rotation modeling. Previously, only the three main moments of inertia (calculated for the loaded aircraft, i.e: including additional weight) were taken into account, while the computed centrifugal (product of inertia) terms were ignored as if they were zero.
- Several issues present in previous versions of the simulation related to rotational dynamics modeling could result in physically incorrect aircraft rotation, especially at high angular velocities. These issues are all resolved using the inertia tensor matrix. The laws of conservation and evolution of angular momentum and rotational kinetic energy are now satisfied with high accuracy.
- Using the inertia tensor means increased limits for angular velocity (up to 10 revolutions per second) and angular acceleration (up to 10 revolutions per second within 0.1 sec) in critical simulation scenarios caused by incorrect flight model settings. These limits serve solely as safeguards to prevent the simulation from crashing and are not expected to be triggered under normal conditions in any simulated scenario.
For these reasons, it is recommended to use the new empty_inertia_tensor parameter instead of the existing empty weight MOI parameters, even if you don't plan to set the optional centrifugal MOI terms or don't know how to calculate them.